مدلسازی قاب فولادی
در این قسمت از آموزش اپنسیس (OpenSees) به بررسی نحوه مدلسازی قاب فولادی میپردازیم. مشخصات تیر و ستونها، نحوه بارگذاری و کلیت مدل در شکل 1 نشان داده شدهاست. همانطور که در شکل مشخص است، قاب فولادی تحت یک بار گسترده 20kN/m در دهانه تیر و دو بار متمرکز 30kN در دو انتهای تیر قرار گرفته است. مشخصات فولاد مصرفی شامل مدول الاستیسیته E = 2e11 N/m2، مقاومت تسلیم فولاد Fy =345 MPa و ضریب سخت شوندگی کرنشی یک درصد (strain hardening ratio = 0.01) میباشد.
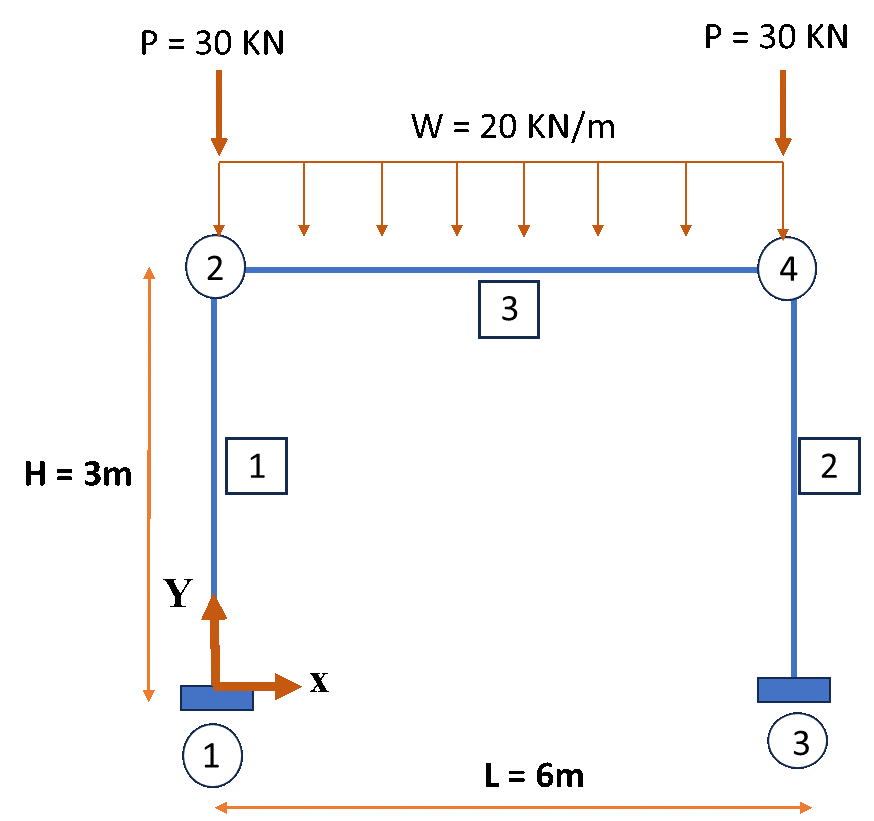
شکل 1. مشخصات قاب فولادی
1 کلیت مدلسازی در OpenSees
در آنالیز اجزاء محدود، مدل مورد بررسی به اجزاء کوچکتری تقسیم میشود که این جزءهای کوچک عناصر محدود نامیده میشوند. به عبارت دیگر زمانی که یک دامنه یا ناحیه هندسی مشبندی میشود، به عناصری گسسته (محدود) تجزیه میشود. هر جزء توسط یک “عنصر(المان)” به جزء مجاور خود در “گرهها” متصل میشود. درواقع یک “گره” نقطهای در فضاست که با “مختصات” تعریف شده و دارای “درجات آزادی” در جهات مختلف است. هر درجه آزادی نیز با توجه به نقش گره در سازه دارای “شرایط مرزی” است. اصل مدلسازی در اپنسیس بر پایه مطالب مطرح شده طبق تحلیل اجزاء محدود است که در ادامه به آن میپردازیم.
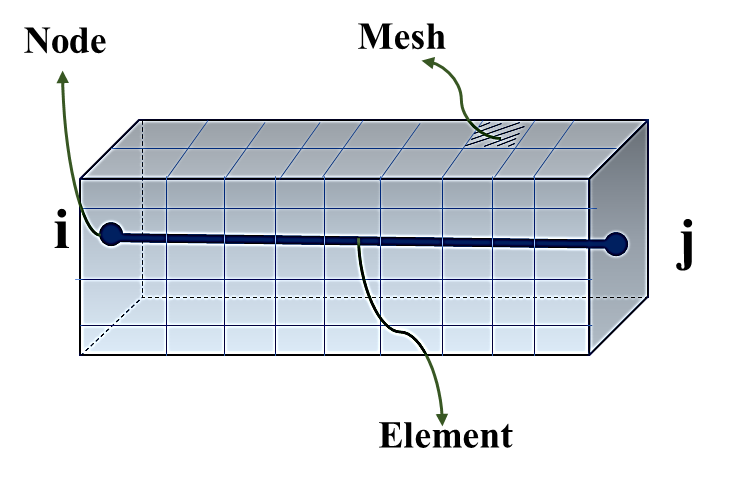
شکل 2. المان مشبندی شده، گره و المان
2 شروع مدلسازی
اولین گام در آموزش Opensees و شروع مدلسازی، شامل مشخص کردن یک دستگاه مختصات کلی برای مدل و همچنین تعیین سیستم اندازهگیری است. توجه داشته باشید که دو پارامتر مطرح شده تا انتهای مدلسازی ثابت بوده و با توجه به فرض کاربر مشخص میشود و خروجیهایی که پس از تحلیل مدل بدست میآید براساس فرض اولیه توسط کاربر است. در این آموزش اپنسیس واحدهای انتخابی طبق واحدهای سیستم SI انتخاب میشوند، یعنی: نیرو = نیوتن و طول = متر. موقعیت مختصات کلی نیز مطابق با مختصاتی است که در شکل 1 نشان داده شدهاست، یعنی جهت مثبت محور y به سمت بالا و جهت مثبت محور x به سمت راست قرار دارد.
در گام بعدی با استفاده از دستور model، ابعاد و تعداد درجات آزادی مدل را مشخص میکنیم.
اپنسیس پایتون:
model ('basic', '-ndm', ndm, '-ndf', ndf)اپنسیس TCL:
model BasicBuilder -ndm $ndm <-ndf $ndf>در این دستور ndm، ابعاد مدل وndf، تعداد درجات آزادی در هر گره را تعیین میکند. باتوجه به اینکه در این آموزش از اپنسیس، قاب دوبعدی، با سه درجه آزادی در هر گره میباشد، این دستور به صورت زیر کدنویسی میشود:
model ('basic', '-ndm', 2, '-ndf', 3)3 تعریف گرهها
برای تعریف گرهها ابتدا باید با توجه به مشخصات و ابعاد قاب فولادی مختصات آنها را تعیین کنیم. در این مدل، باتوجه به شکل 1، به چهار گره نیاز داریم که باید مختصات آنها مشخص شوند. به منظور تعیین راحتتر مختصات گرهها ارتفاع و عرض قاب فولادی را مشخص میکنیم:
H = 3m
L = 6 mH و L به ترتیب بیانگر ارتفاع قاب و عرض دهانه است. دستور تعریف گرهها node میباشد که ورودیهای این دستور از قرار زیر است:
اپنسیس پایتون:
node(nodeTag, *crds)اپنسیس TCL:
node $nodeTag (ndm $coords) <-mass (ndf $massValues)>در این دستور nodeTag شماره گره و *crds مختصات گره را نشان میدهد. در این مثال مطابق با شکل 1 مختصات گرهها بصورت زیر تعریف میشود:
node (1, 0, 0)
node (2, 0, H)
node (3, L, 0)
node (4, L, H)
4 تعیین غیرخطی هندسی
همانطور که میدانیم اثرات غیرخطی را در دو حالت میتوان درنظر گرفت. در حالت اول اثر P-Δ بزرگ و یا به عبارتی رفتار غیرخطی هندسی را داریم. در این حالت مطابق با شکل 3، یک ارتباط غیرخطی بین نیروی P و تغییرشکل Δ برقرار است. بدین صورت که با افزایش نیروی P1 تغییر مکان Δ افزایش یافته و بنابراین لنگر ناشی از نیروی P2 نیز افزایش پیدا میکند و همین افزایش لنگر سبب افزایش مجدد Δ میشود که اصطلاحاً به این حالت اثر P-Δ یا لنگر ثانویه میگویند. مورد بعدی رفتار غیرخطی متریال است. بدین صورت که هر متریال پس از گذر از ناحیه رفتار الاستیک، وارد شاخهای با سختی کمتر نسبت به سختی اولیه شده و رفتار آن از حالت خطی خارج میشود. مانند رفتار فولاد که در بخش بعدی به آن پرداخته شدهاست. بنابراین در مرحله بعدی از آموزش OpenSees، برای پیشبرد مراحل ابتدا لازم است geomTransf که بیانگر نوع غیرخطی هندسی است را مشخص کنیم. در این آموزش نوع غیرخطی هندسی را از نوع Pdelta درنظر میگیریم. بنابراین از دستور زیر استفاده میکنیم:
اپنسیس پایتون:
geomTransf ('PDelta', transfTag)اپنسیس TCL:
geomTransf PDelta $transfTag <-jntOffset $dXi $dYi $dXj $dYj>کدنویسی این دستور به صورت زیر انجام شده و تگ مربوط به آن برابر با یک درنظر گرفته میشود:
transfTag = 1
geomTransf ('PDelta', transfTag)
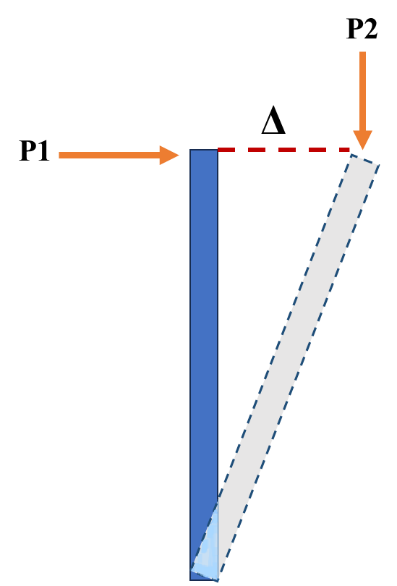
شکل 3. اثر لنگر ثانویه روی ستون
5 تعریف متریال
در ادامه مدلسازی باید مشخص کنیم که جنس متریال المانهای سازه چیست، به طور مثال سازه ما از نوع فولادی یا بتنی است. باتوجه به اینکه در این قسمت از آموزش اپنسیس، هدف یادگیری مدلسازی قاب فولادی است، بنابراین از متریال فولادی نیز استفاده میشود. از بین متریالهای فولادی مختلفی که در سایت اپنسیس ارائه شدهاست، متریال فولادی قاب را از نوع steel02 انتخاب میکنیم که دستور آن به شرح زیر است:
اپنسیس پایتون:
uniaxialMaterial('Steel02', matTag, Fy, E0, b, *params, a1=a2*Fy/E0, a2=1.0, a3=a4*Fy/E0, a4=1.0, sigInit=0.0)اپنسیس TCL:
uniaxialMaterial Steel02 $matTag $Fy $E $b $R0 $cR1 $cR2 <$a1 $a2 $a3 $a4 $sigInit>نمودار رفتاری این متریال مطابق با شکل 4 میباشد.
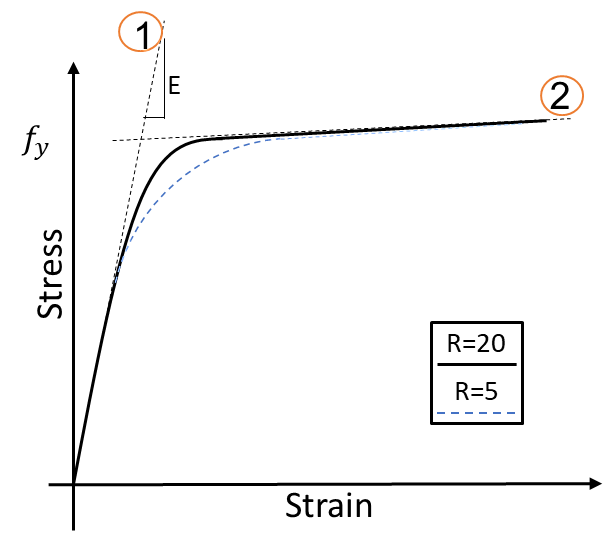
شکل 4. نمودار رفتاری فولاد steel02
این دستور علاوه بر شماره تگ، مقاومت تسلیم (Fy)، مدول الاستیسیته (E)، سخت شوندگی کرنشی (b) و پارامترهایی که انتقال رفتار فولاد از شاخه الاستیک به پلاستیک را کنترل میکنند (R0, cR1, cR2) را نیز به عنوان ورودی از کاربر میگیرد.
سخت شوندگی کرنشی یا پارامتر hardeningRatio نسبت سختی ثانویه به سختی اولیه است. مطابق با شکل 4، خط شماره یک سختی اولیه (شیب ناحیه الاستیک) و خط شماره دو (شیب نمودار در قسمت نرم شده) سختی ثانویه را نشان میدهد. در این مثال این نسبت 0.01 درنظر گرفته شدهاست. یعنی اگر سختی اولیه فولاد Es = 2e11 N/m2 باشد، سختی ثانویه فولاد به میزان یک درصد این سختی است. همچنین مقادیر پیشنهادی لیست parameters، در سایت اپنسیس عنوان شده که میتوانند بصورت زیر تعریف شوند:
R0 = 18; cR1 = 0.925; R2 = 0.15درنهایت ورودیهای این دستور در این مثال به صورت زیر تعریف میشوند:
steelMatTag = 1
Fy = 345e6
Es = 2e11
hardeningRatio = 0.01
R0 = 18; cR1 = 0.925; R2 = 0.15
uniaxialMaterial('Steel02', steelMatTag, Fy, Es, hardeningRatio, R0, cR1, R2)6 تعریف مقطع
در ابتدا به منظور مدلسازی مقاطع تیر و ستون در اپنسیس از مقاطع فایبر (fiber section) استفاده میکنیم. سپس به دستورات قسمت patch که برای مدلسازی انواع مقاطع مستطیلی، دایرهای و … به کار میرود مراجعه کرده و بدین منظور دستور زیر را به کار میگیریم:
اپنسیس پایتون:
section('Fiber', secTag)
patch('quad', matTag, numSubdivIJ, numSubdivJK, *crdsI, *crdsJ, *crdsK, *crdsL)اپنسیس TCL:
section )Fiber, secTag ({
patch (quad, matTag, numSubdivIJ, numSubdivJK, yI, zI, yJ, zJ, yK, zK, yL, zL)}
1-6 محورهای محلی
همانطور که از تحلیل اجزاء محدود میدانیم، نیروهای داخلی عناصر محدود پس از تحلیل در راستای محور محلی المان نشان داده میشوند. در نرم افزار اپنسیس فرض جهت محورهای محلی با کاربر بوده و باید به صورت دقیق تعیین شود. بنابراین قبل از تعریف مقطع مورد نظر باید محورهای محلی را روی آن درنظر بگیریم. به کمک شکل 5، نحوه تعیین محورهای محلی را به طور مختصر شرح میدهیم. به طور کلی یک سیستم مختصات محلی توسط محورهای y ،x و z هر المان و همچنین موقعیت مبدأ مختصات مشخص میشود. اگر ستون A از نقطه i به سمت j رسم شده باشد، محور x محلی از پایین به بالا و در راستای ترسیم شدهاست. در واقع همواره محور محلی x در راستای ترسیم i به j است. از طرفی محور محلی z در مدل دوبعدی همواره به سمت خارج صفحه (به سمت ما) و منطبق بر محور z کلی خواهد بود. در این حالت محور y به کمک قانون دست راست بدست میآید که در این مثال این محور به سمت چپ قرار میگیرد.
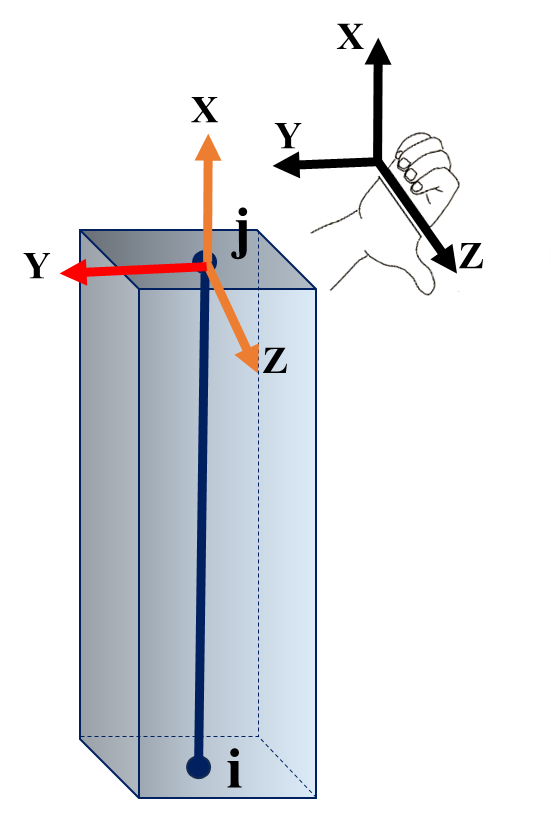
شکل 5. ستون A و نمایش محورهای محلی
باتوجه به نکات مطرح شده، به عنوان تمرین، محور محلی تیر B نشان داده شده در شکل 6 را درحالت دوبعدی بدست آورید. اگر جهت ترسیم تیر از سمت چپ به راست و از نقطه i به سمت نقطه j باشد، محور y به کدام سمت خواهد بود؟
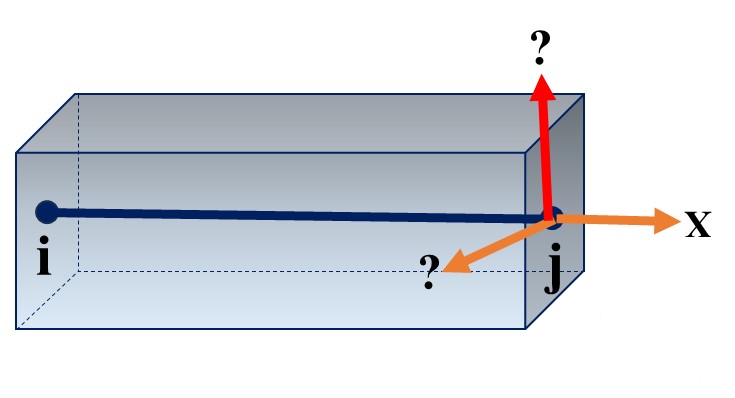
شکل 6. تیر B و محورهای محلی
نکته بعد درخصوص قرارگرفتن مبدأ مختصات محلی روی المان است. به شکل 5 دقت کنید. اگر از بالا به این ستون نگاه کنیم محور y محلی به سمت بالا و محور z محلی به سمت چپ قرار میگیرد. از آنجایی که موقعیت مبدأ مختصات روی پاسخ بیتأثیر است، میتوان آن را در هر نقطه دلخواه درنظر گرفت. بنابراین مطابق با شکل 7، در این آموزش OpenSees، محور محلی y به سمت بالا و محور محلی z به سمت چپ و مبدأ مختصات نیز در مرکز مقطع درنظر گرفته میشود.
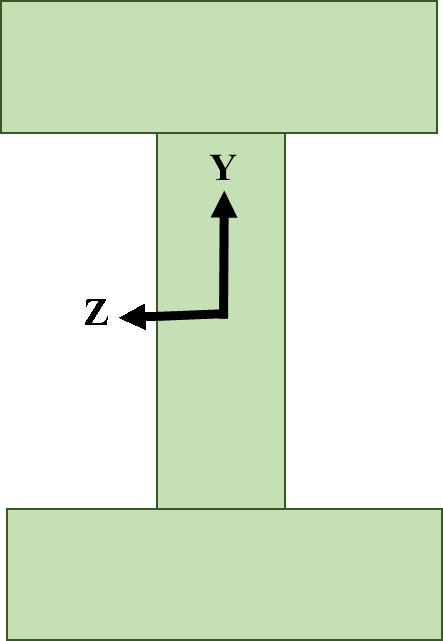
شکل 7. موقعیت مبدأ مختصات محلی روی المان
2-6 مختصات رئوس قطعات
یک تیر I شکل را درنظر بگیرید. مطابق با شکل 8 میتوان گفت که این تیر از سه قطعه مستطیلی شکل تشکیل شدهاست. هرشکل مستطیلی چهار گوشه دارد که به صورت پادساعتگرد و با حروف k ،j ،i و l مطابق با شکل 8 نامگذاری شده و مختصات این نقاط نیز با توجه به مبدأ مختصات محلی و ابعاد مقطع تعیین میشود. دستور patch در اپنسیس مختصات این نقاط را از کاربر میگیرد که در دستور اپنسیس با پارامترهای (yI zI yJ zJ yK zK yL zL) نشان داده شده است.
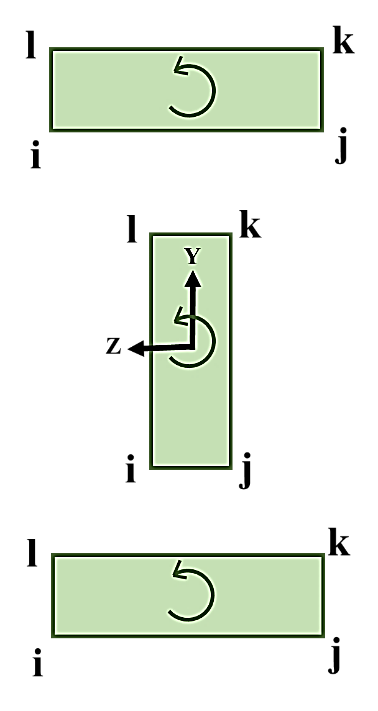
شکل 8. نحوه درنظر گرفتن k ،j ،i و l مختصات محلی مقطع
7 تقسیم بندی مقطع
مرحله بعد در آموزش OpenSees مشبندی و تقسیم مقطع به زیربخش (فایبر) در دوجهت متعامد است. بدین منظور دو پارامتر زیر در دستور patch مورد بررسی و استفاده قرار میگیرد. این دو پارامتر مشخص میکند که مقطع به ترتیب در راستای ij و در راستای jk به چند قسمت تقسیم شود که این تقسیمبندی نیز به صورت دلخواه صورت میگیرد.
numSubdivij
numSubdivjkباتوجه به اینکه در این مثال از آموزش اپنسیس، از مقطع W12x40 استفاده شدهاست، دستور مقطع فایبر باتوجه به شکل 8 برای قسمت A که بال بالایی مقطع میباشد به صورت زیر تعریف میشود.
# W12x40
colSecTag = 1
d = 0.3023
bf = 0.2035
tf = 0.0131
tw = 0.0075
section(‘Fiber’, colSecTag)
patch(‘quad’, matTag, numSubdivij, numSubdivjk, d/2-tf, bf/2, d/2-tf, -bf/2, d/2, -bf/2, d/2, bf/2)دقت داریم که دستور patch برای دو قسمت مستطیلی دیگر نیز به همین ترتیب تعریف شده و در مجموع سه قسمت مستطیلی که مقطع را میسازند با دستور patch تقسیمبندی و مختصاتدهی میشوند. دقت شود از آنجایی که متریال این مقطع از نوع فولادی است، به جای matTag از steelMatTag استفاده میکنیم.
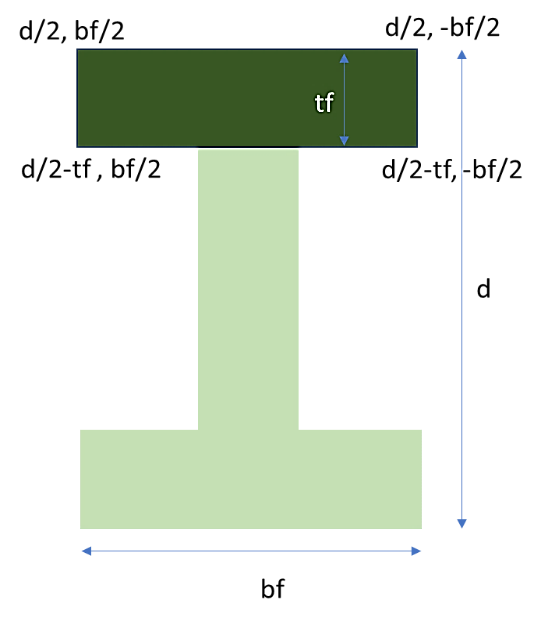
شکل 9. مقطع ستون I شکل قاب فولادی و مختصات نقاط ijkl بال بالایی مقطع.
تعریف مقطع تیر قاب فولادی نیز عیناً مشابه با تعریف ستون بوده و تنها مشخصات مقطع تغییر پیدا میکند و به صورت زیر تعریف میشود.
#W12x40
beamSecTag = 2
d = 0.3023
bf = 0.2035
tf = 0.0131
tw = 0.00758 تعریف المان
پس از تعریف مقطع، باید المان مناسب را جهت اختصاص مقاطع تیر و ستون تعریف شده به آن مشخص کنیم. در این آموزش اپنسیس با توجه به اینکه قاب فولادی از نوع غیرخطی میباشد، از بخش element commands ، قسمت Beam-Column Elements المان forceBeamColumn را انتخاب میکنیم که دستور آن به صورت زیر میباشد:
اپنسیس پایتون:
element('forceBeamColumn', eleTag, *eleNodes, transfTag, integrationTag, '-iter', maxIter=10, tol=1e-12, '-mass', mass=0.0)اپنسیس TCL:
element forceBeamColumn $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag <-mass $massDens> <-iter $maxIters $tol> <-integration $intType>در این دستور ابتدا تگ المان و سپس گرههای دوسر المان مشخص میشود. دستور transfTag که پیشتر تعریف شده بود و integrationTag نیز به ترتیب به المان اختصاص مییابد.
integrationTag : هنگامی که المان از نوع فایبر مدل میشود، نقاطی موسوم به نقاط انتگرالگیری داریم که پاسخهای غیرخطی در این نقاط انتگرالگیری یا نقاط گوس محاسبه میشوند. بنابراین دستور beamIntegration بدین منظور استفاده میشود. این دستور از کاربر میخواهد تعداد نقاط انتگرالگیری و همچنین مقطعی که انتگرالگیری روی آن صورت میگیرد را وارد کند. در دستورات اپنسیس چندین روش انتگرالگیری ارائه شدهاست که ما از روش Lobatto استفاده میکنیم. دستور این روش از قرار زیر میباشد:
beamIntegration('Lobatto', secTag, secTag, N)در این دستور N تعداد نقاط انتگرالگیری و secTag به ترتیب بیانگر تگ نقاط انتگرالگیری (که دلخواه است) و مقطعی که روی آن محاسبات انتگرالگیری در نقاط مذکور صورت میگیرد میباشد که برای تیر و ستون به صورت زیر تعریف میشود.
numIntgrPts = 5
beamIntegration('Lobatto', beamSecTag, beamSecTag, numIntgrPts)
beamIntegration('Lobatto', colSecTag, colSecTag, numIntgrPts)حال به تعریف المان تیر و ستونها میپردازیم و پارامترهای تعریف شده را به دستور المان اختصاص میدهیم:
element('forceBeamColumn', 1, 1, 2, transfTag, colSecTag)
element('forceBeamColumn', 2, 3, 4, transfTag, colSecTag)
element('forceBeamColumn', 3, 2, 4, transfTag, beamSecTag)9 شرایط مرزی
همان طور که در ابتدا اشاره شد، گرهها، المانها، درجات آزادی و شرایط مرزی از مفاهیم بسیار مهمی در تحلیل اجزاء محدود هستند. تا این قسمت از آموزش OpenSees سه مورد اول تعیین شدند و مورد بررسی قرار گرفتند. بنابراین در این بخش از آموزش اپنسیس به تعیین شرایط مرزی گرهها و تکیهگاه قاب فولادی میپردازیم. به طور کلی شرایط مرزی بیانگر این مفهوم است که هر گره با توجه به اینکه جزِئی از یک سیستم پیوسته است و همچنین با توجه به عملکرد سازهای و نقش آن در سازه، در درجات آزادی خاصی مقید میشود. از آنجایی که تقید هرکدام از درجات آزادی منجر به تشکیل نیرو در همان درجه آزادی میشود، باید با دقت و به درستی تعیین شود تا در نهایت خروجیهای صحیحی پس از تحلیل مدل به دست آید. از طرفی در تحلیل اجزاء محدود، درجات آزادی میتوانند اشکال گوناگونی به خود بگیرند. به طور مثال در تحلیل سازه درجات آزادی از جنس جابهجایی هستند، در حالی که در تحلیل حرارتی درجه آزادی از جنس دما است. در این مثال، با توجه به اینکه مدلسازی به صورت دوبعدی است، سه درجه آزادی شامل دو درجه آزادی انتقالی و یک درجه آزادی دورانی داریم. باتوجه به شکل 1، گره یک و سه، تکیهگاه قاب فولادی بوده و گره دو و چهار عضوی از سیستم پیوسته مدل هستند. بنابراین کافیست تنها شرایط مرزی دو گره یک و سه را مشخص کنیم. در اپنسیس دستور fix برای تعیین شرایط مرزی گرهها به کار میرود که از قرار زیر میباشد:
اپنسیس پایتون:
fix (nodeTag, *constrValues)اپنسیس TCL:
fix $nodeTag (ndf $constrValues)در این دستور ابتدا تگ گره مورد نظر و سپس شرایط گره در درجات آزادی مربوطه را وارد میکنیم. که در این مثال به صورت زیر تعریف میشود:
fix (1, 1, 1, 1)
fix (3, 1, 1, 1)عدد اول بیانگر تگ گرهای که شرایط مرزی به آن اختصاص مییابد بوده و سه عدد بعدی نشاندهنده شرایط گره در فضا است. عدد یک به معنای تقید گره و عدد صفر به معنای آزاد بودن گره در آن درجه آزادی است. در این مثال گره یک و گره سه، تکیهگاه سازه بوده و از نوع گیردار میباشد. بنابراین هر دو گره، باتوجه به دوبعدی بودن سازه در سه درجه آزادی خود مقید میشوند.
10 الگوی بار
بعد از اینکه مدلسازی کلی به اتمام رسید و شمای کلی مدل شامل ابعاد، متریال مصرفی، مقاطع، المانها و شرایط مرزی و تکیهگاهی مشخص شد، به سراغ بارگذاری مدل و تعیین شرایط اعمال بار میرویم. به منظور اعمال بار به قسمت pattern commands سایت اپنسیس مراجعه میکنیم. دقت داریم که درحال بارگذاری ثقلی هستیم و بارگذاری ثقلی مدل از طریق دستورات بخش Plain pattern اعمال میشود. دستور کلی جهت اعمال بار ثقلی در سایت اپنسیس به صورت زیر میباشد:
اپنسیس پایتون:
pattern('Plain', patternTag, tsTag, '-fact', fact)اپنسیس TCL:
pattern Plain $patternTag $tsTag <-fact $cFactor>ورودیهای این دستور شامل شماره تگ الگو (patternTag)، تگ سری زمانی (tsTag) و ضریب اعمال بار (fact) میباشد.
1-10 سری زمانی
همان طور که میدانید زمان در تحلیل دینامیکی یک مفهوم واقعی دارد و در واقع تفاوت اصلی حالت دینامیکی نسبت به حالت استاتیکی، تغییر شرایط نسبت به زمان است. مثلاً در حالت دینامیکی بارگذاری در طول زمان تغییر میکند اما در حالت استاتیکی بارگذاری ثابت است و یا به طور مثال با مشتق جابجایی نسبت به زمان، سرعت به دست میآید. اما در حالت استاتیکی زمان یک مفهوم مجازی دارد و مشخص میکند که بارگذاری در هر مرحله با چه ضریبی به سازه اعمال شود. تعیین این ضریب به هنگام تعیین دستورات ثقلی و توسط دستور integrator انجام میشود که در بخش تحلیل به آن پرداخته میشود. اما در خصوص شرایط و نحوه اعمال، باید اشاره کرد که اپنسیس نحوه اعمال این ضریب را به طرق متفاوتی درنظر میگیرد. یکی از این حالات شرایط خطی یا linear است. درحالت linear ضریب گام بارگذاری آرام آرام و بصورت خطی افزایش مییابد و در نهایت به عدد یک میرسد. این دستور در اپنسیس به صورت زیر است:
اپنسیس پایتون:
timeSeries('Linear', tag, '-factor', factor=1.0, '-tStart', tStart=0.0)اپنسیس TCL:
timeSeries Linear $tag <-factor $cFactor>همان طور که در دستور نیز مشخص است، به جز تگ سری زمانی دو پارامتر factor و tStart نیز قید شده، که دارای مقدار هستند. این بدین معنی است که اگر در دستور مقدار آن توسط کاربر ذکر نشده باشد، مقادیر عنوان شده بصورت پیشفرض توسط نرمافزار درنظر گرفته میشود. کدنویسی این دستور به صورت زیر انجام میشود:
linearSeriesTag = 1
timeSeries('Linear', linearSeriesTag)
بنابراین دستور بارگذاری مدل در نهایت به شکل زیر تعریف میشود:
pattern('Plain', 1, linearSeriesTag)حال با توجه به اینکه بارگذاری روی گره اعمال میشود یا روی المان، از یکی از دستورات load command یا eleload command استفاده میکنیم. با توجه به اینکه در این مثال از آموزش اپنسیس دو بار متمرکز روی گرههای دو و چهار و همچنین یک بار گسترده روی المان شماره سه (طبق شکل 1) داریم، بنابراین از هر دو دستور استفاده میکنیم.
2-10 بارگذاری متمرکز گرهای
دستور بارگذاری گرهای در اپنسیس به صورت زیر میباشد:
اپنسیس پایتون:
load(nodeTag, *loadValues)اپنسیس TCL:
load $nodeTag (ndf $LoadValues)در این دستور در هر درجه آزادی بار مورد نظر (loadValues) به گره دلخواه (nodeTag) وارد میشود. در این مرحله حتماً باید به واحد نیرو که در ابتدا توسط کاربر فرض شدهاست، دقت شود. بنابراین بارگذاری گرههای دو و چهار به شکل زیر تعریف میشود:
load(2, 0, -30e3, 0)
load(4, 0, -30e3, 0)
همان طور که اشاره شد، بارگذاری در تمام درجات آزادی صورت میگیرد. در این مثال هر گره سه درجه آزادی دارد و تنها در درجه آزادی دوم (خلاف جهت y) بار داریم، بنابراین با توجه به اینکه بارگذاری گرهای براساس محور مختصات کلی (Global) صورت میگیرد، بارگذاری با علامت منفی (به سمت پایین) اعمال میشود.
3-10 بارگذاری گسترده روی المان
بارگذاری بعدی روی المان صورت میگیرد و مقدار آن 20kN/m میباشد. پس باید از دستور بارگذاری المانی دوبعدی که در زیر به آن اشاره شدهاست استفاده کنیم:
اپنسیس پایتون:
eleLoad('-ele', *eleTags, '-type', '-beamUniform', Wy, Wx=0.0)اپنسیس TCL:
eleLoad -ele $eleTag1 <$eleTag2 ....> -type -beamUniform $Wy <$Wx>این دستور تگ المانی که تحت بارگذاری قرار دارد (eleTags)، نوع بار (type) و مقدار بار در هر جهت از محور مختصات محلی المان را به عنوان ورودی از کاربر میگیرد. در این مثال المان شماره سه خلاف جهت y دارای بار گسترده یکنواخت میباشد. پس کدنویسی به صورت زیر انجام میشود:
Wy = 20e3
eleLoad('-ele', 3, '-type', '-beamUniform', -Wy)11 تعیین خروجیها
تا به این بخش از آموزش OpenSees مدل تعریف شده و بارگذاری آن نیز صورت گرفته است. مرحله بعدی تعیین خروجیهای موردنظر در نرمافزار است. دقت داشته باشید که بر خلاف نرمافزارهای متداول مانند Etabs که خروجیهای ثابت داشته و پس از تحلیل قابل دسترسی است، در نرمافزار اپنیسیس تعداد، جزئیات و نوع خروجیها توسط کاربر تعیین میشود. بنابراین برای اینکه خروجیهای موردنظر ثبت شود، باید قبل از تحلیل ثقلی مدل، این خروجیها توسط کاربر تعیین و مشخص شود. در واقع این دستور تحلیلهایی که بعد از آن قرار دارد را ضبط و ذخیره میکند. به سایت اپنسیس مراجعه کرده و وارد بخش Output Commands میشویم. در این قسمت از بین گزینههای مختلفی که قرار دارد، گزینه recorder command را انتخاب میکنیم. این گزینه چندین نوع مختلف از خروجی را به ما ارائه میدهد. خروجیهای مدنظر ما شامل تغییر شکل گره دو، عکسالعملهای تکیهگاهی گره یک و گره سه، خروجیهای مربوط به المان تیر و هر دو ستون میباشد.
1-11 خروجی گرهای
دستور خروجی که از گره (Node) میتوان گرفت به صورت زیر میباشد:
اپنسیس پایتون:
recorder('Node', '-file', filename, '-node', *nodeTags=[], '-dof', *dofs=[], respType)اپنسیس TCL:
recorder Node <-file $fileName> <-node $node1 $node2 ...> -dof ($dof1 $dof2 ...) $respType'ورودیهایی که باید مشخص کنیم عبارت اند از نام فایل (file)، شماره گره (node)، درجه یا درجات آزادی (dof) که میخواهیم از آن خروجی بگیریم و همچنین نوع پاسخی (respType) که مد نظر است. خروجی مربوط به گره شماره دو به شکل زیر تعریف میشود:
recorder('Node', '-file', 'disp.txt', '-node', 2, '-dof', 1, 2, 3, 'disp')عکسالعملهای تکیهگاهی شامل به ترتیب برش Vx، نیروی Fy و لنگر Mz بصورت زیر تعیین میشود:
recorder('Node', '-file', 'Vx.txt', '-node', 1, 3, '-dof', 1, 'reaction')
recorder('Node', '-file', 'Fy.txt', '-node', 1, 3, '-dof', 2, 'reaction')
recorder('Node', '-file', 'Mz.txt', '-node', 1, 3, '-dof', 3, 'reaction')
2-11 خروجی المانی
دستور خروجی که از المان (element) میتوان گرفت به صورت زیر میباشد:
اپنسیس پایتون:
recorder('Element', '-file', filename, '-ele', *eleTags=[], *args)اپنسیس TCL:
recorder Element <-file $fileName> <-ele ($ele1 $ele2 ...)> $arg1 $arg2 ...ورودیهای مورد نیاز این دستور نیز شامل نام فایل (filename)، شماره المان (eleTags) و نوع خروجی (args) میباشد. نوع خروجی هر المان به نوع المان بستگی دارد و در صفحهای که دستور المان قرار گرفته، پاسخهایی که میشود از آن المان به دست آورد نیز ذکر شدهاست. خروجی مربوط به تیر و ستونها به ترتیب به صورت زیر کدنویسی میشود:
recorder('Element', 'beamForce.txt', '-ele', 3, 'localForce')
recorder('Element', 'columnForce.txt', '-ele', 1, 2, 'localForce')
12 تحلیل ثقلی
نوبت به تحلیل مدل تحت بارهای ثقلی میرسد. بدین منظور وارد سایت اپنسیس شده و به بخش Analysis command مراجعه میکنیم. از بین دستورات مختلفی که در این بخش قرار دارد، سه دستور اساسی که بدون آنها تحلیل انجام نمیشود و حتماً باید توسط کاربر مشخص شود، عبارت اند از: integrator commands ،analysis command و analyze command. تعیین باقی دستورات اختیاری است و اگر کاربر آنها را تعیین نکند، خود نرمافزار مقادیر پیشفرضی را برای آنها درنظر میگیرد.
1-12 integrator command
این دستور روش تحلیل را مشخص میکند که به دو بخش استاتیکی (Static) و دینامیکی (Transient) تقسیم میشود. آنچه که ما برای تحلیل ثقلی به آن نیاز داریم دستور loadcontrol زیرمجموعه دستورات استاتیکی است.
اپنسیس پایتون:
integrator('LoadControl', incr)اپنسیس TCL:
integrator LoadControl $lambda <$numIter $minLambda $maxLambda>همان طور که پیشتر نیز مطرح شد، در این دستور گام بارگذاری مشخص شده و توسط incr مقداردهی میشود.
2-12 analysis command
این دستورکه نحوه تحلیل مدل را مشخص میکند، به صورت زیر میباشد:
اپنسیس پایتون:
analysis(analysisType)اپنسیس TCL:
analysis analysisType? ورودی analysisType از ما نوع تحلیل را میخواهد که با توجه به اینکه تحلیل ثقلی است، باید از دستور Static بدین منظور استفاده کرد.
3-12 analyze command
این دستور برای اجرای تحلیل است و تا زمانی که بکار نرود تحلیل اجرا نمیشود.
اپنسیس پایتون:
analyze(numIncr=1)اپنسیس TCL:
analyze $numIncr در دستور analyze مشخص میکنیم که تحلیل در چند گام انجام میشود. ازطرفی در دستور integrator ضریبی که بارگذاری در هر گام افزایش پیدا میکند را مینویسیم. به طور پیشفرض بارگذاری در یک مرحله صورت میگیرد که میتوان تعداد گام بارگذاری را با توجه به افزایش گام به گام آن توسط دستور integrator تنظیم کرد.
تحلیل ثقلی به کمک همین سه دستور صورت میگیرد و باقی دستورات توسط نرمافزار فرض میشود. در این آموزش OpenSees به طور کلی دستورات تحلیل ثقلی به شکل زیر تعریف میشود:
wipeAnalysis()
constraints('Transformation')
numberer('RCM')
system('BandGen')
test('NormDispIncr', 1e-6, 100)
algorithm('Newton')
integrator('LoadControl', 0.1)
analysis('Static')
analyze(10)
loadConst('-time', 0)
نکته:
دستور ()wipe همیشه قبل و بعد از مدل در انتهای تحلیل ثقلی نوشته میشود. زیرا در غیر اینصورت خروجیها به شکل واقعی داخل فایلها قرار نگرفته و فایلها بسته نمیشود.
13 زمان تناوب
پریود یا زمان تناوب یک ویژگی ذاتی در سازه و کمیتی وابسته به جرم و سختی است. بنابراین برای محاسبه آن، نیاز به ماتریس جرم و ماتریس سختی داریم. ماتریس سختی با توجه به المانهایی که برای سازه تعریف کردیم مشخص میشود. ماتریس جرم نیز در بخش بعدی توضیح داده شدهاست. از دینامیک سازه به خاطر داریم که با تحلیل eigen و تشکیل معادلهی مشخصه (characteristic equation) با ماتریس جرم و سختی به شکل زیر:
|k-mω²|=0
توان دوم مقادیر فرکانس دورانی یا ω² به دست میآید. از طرفی زمان تناوب برابر است با:
T=2π/ω
بنابراین کافیست تا پس از محاسبه جرم و اختصاص آن به گرهها، زمان تناوب سازه را به کمک رابطه بالا محاسبه کنیم.
1-13 جرم
میدانیم که جرم حاصل از بارهای ثقلی است. بنابراین کافیست پس از محاسبهی بارهای ثقلی، آنها را به شتاب گرانش زمین تقسیم کنیم تا جرم به دست آید. در این مثال دو بار متمرکز 30kN و یک بار گسترده یکتواخت 20kN/m در دهانه 6 متری قاب وارد میشود که مجموعاً معادل 180kN بار است. با تبدیل این بار به نیوتن و تقسیم آن به شتاب گرانش زمین درنهایت 18348.6kg جرم به دست میآید. با توجه به اینکه میخواهیم به دو گرهی شمارهی دو و چهار جرم اختصاص دهیم، پس باید جرم کل به دست آمده را تقسیم بر دو کنیم تا سهم هر گره مشخص شود. در نهایت مقدار 9174.31kg جرم برای هر گره حاصل میشود. در اپنسیس دستور اختصاص جرم به گره مطابق دستور زیر میباشد:
mass(nodeTag, *massValues)بدین صورت که ابتدا گره موردنظر (nodeTag) و سپس مقدار جرم در هر درجه آزادی (massValues) را وارد میکنیم. در این مثال با توجه به اینکه مدلسازی به صورت دوبعدی صورت گرفتهاست، اختصاص جرم در دو درجه آزادی انتقالی صورت میگیرد و در درجه آزادی دورانی مقداری ناچیز و یا مقدار صفر وارد میشود:
mass(2, 9174.3, 9174.3, 0)
mass(4, 9174.3, 9174.3, 0)
طبق توضیحات مطرح شده، پس از تعریف و تعیین میزان جرم، حال میتوانیم مقدار پریود سازه را به دست بیاوریم.
2-13 مقادیر ویژه
وارد قسمت Analysis commands در سایت اپنسیس شده و به بخش eigen command مراجعه میکنیم.
eigen(solver='-genBandArpack', numEigenvalues)این دستور طریقه حل (solver) و همچنین تعداد مودهایی که مقادیر ویژه را برای آن محاسبه میکند (numEigenvalues) از کاربر دریافت میکند که مورد اول اختیاری است.
نکته:
تعداد مودهایی که میتوانیم تعریف کنیم برابر است با تعداد درجات آزادی جرمدار منهای یک.
جهت سهولت کار، مقادیر ویژه را در متغیری به نام omega2List ذخیره میکنیم و در نهایت دستور تعیین مقادیر ویژه به صورت زیر کدنویسی میشود:
omega2List = eigen(2)به منظور محاسبه پریود در هر مود، یک حلقه به صورت زیر ایجاد میکنیم:
for omega2 in omega2List:
omega = math.sqrt(omega2)
T = 2*math.pi/omega
print(T)
در این حلقه ابتدا جذر هر مقدار ویژه در متغیر omega ذخیره میشود. طبق رابطهای که داشتیم (T=2π/ω)، پریود برای هر مود محاسبه و نمایش داده میشود.
14 تفسیر نتایج
پس از اتمام مدلسازی، تعریف رکوردرها برای دریافت خروجیهای موردنظر و تحلیل مدل، نوبت به بررسی و تفسیر نتایج به دست آمده میباشد. در این مثال از آموزش اپنسیس، خروجیهای متداول مربوط به گرهها، ستونها و تیر مورد بررسی قرار گرفت که تفسیر هر خروجی به شرح زیر است:
14-1 خروجی گرهها
در خروجیهایی که از گرهها میگیریم، پاسخها براساس محور مختصات کلی به دست میآیند، اما در خروجیهایی که از المان میگیریم نوع پاسخ توسط کاربر مشخص میشود. به طور مثال اگر در رکوردر المان بجای localforce از force استفاده کنیم، خروجیهای حاصل نیز از حالت مختصات محلی به مختصات کلی تغییر پیدا میکنند. طبق رکوردرهای تعریف شده برای گرهها، پاسخهای به دست آمده پس از تحلیل به شرح زیر میباشد:
جدول1. پاسخهای به دست آمده برای گرهها
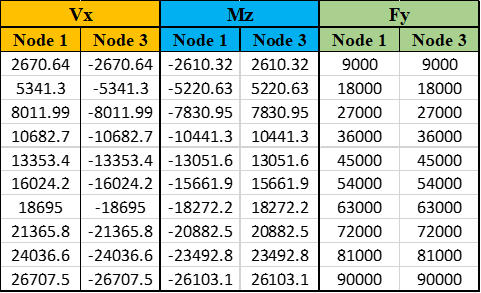
همان طور که در جدول 1 نشان داده شدهاست برای هر دسته پاسخ، ستون اول مربوط به گرهی شمارهی یک و ستون دوم پاسخهای مربوط به گرهی سوم میباشد. همان طور که در بخش تحلیل ثقلی به آن پرداخته شد، تحلیل در ده گام با گامهای 0.1 صورت گرفت. بنابراین ده سطر از پاسخ برای هر خروجی داریم که ناشی از اعمال افزایشی بار با ضریب 0.1 میباشد. برش پایه کل ناشی از بارگذاری، مجموع مقادیر سطر دهم در هر ستون میباشد. در این حالت بار با ضریب یک به سازه اعمال شدهاست. در مثال مورد بررسی، با توجه به اینکه بارگذاری قائم بوده و هیچگونه بار افقی به سازه اعمال نشدهاست، بنابراین برش پایه کل برابر با صفر بدست میآید. همچنین مقادیر لنگر بدست آمده نیز به همین ترتیب مقدار صفر را به دست میدهد. از طرف دیگر مقدار نیروی 180kN و برابر با بار قائم بدست میآید. بنابراین طبق تعادل در راستای قائم صحت مدلسازی در نتایج بدست آمده از تحلیل مدل مشهود است.
14-2 خروجی ستون ها
از ستونها خروجی بر اساس محور مختصات محلی گرفته شدهاست.کل پاسخهای به دست آمده طبق جدول 2 میباشد.
جدول2. پاسخهای به دست آمده برای ستونها
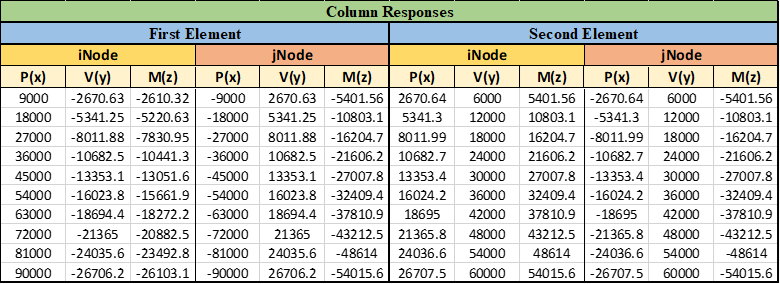
همانطور که در بخش خروجیهای گرهی توضیح داده شد، ده سطر خروجی برای ستونها به دست میآید. با توجه به اینکه برای دو المان ستون خروجی گرفتیم و در هر گره که دو سر المان قرار گرفته سه درجه آزادی داریم، شش ستون اول مربوط به المان اول و شش ستون دوم مربوط به المان دوم است. برای هر المان سه ستون اول پاسخهای گره i و سه ستون دوم پاسخهای گره j میباشد. همچنین درجه آزادی اول نیرو در جهت x محلی، درجه آزادی دوم برش y محلی و درجه آزادی سوم لنگر حول z محلی را نشان میدهد.
14-3 خروجی تیر
پاسخهای به دست آمده برای تیر مطابق با جدول 3 میباشد.
جدول3. پاسخهای به دست آمده برای تیر
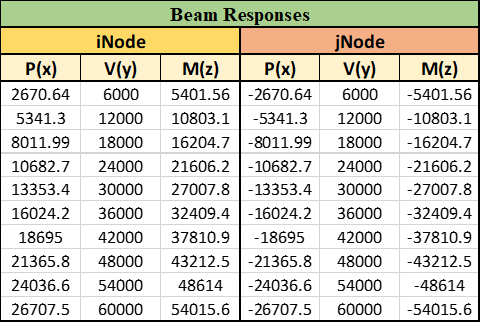
تفسیر نتایج به دست آمده برای تیر مشابه با نتایج ستون میباشد. بدین صورت که سه ستون اول مربوط به پاسخهای گره i و سه ستون بعدی پاسخهای مربوط به گره j است. همچنین باقی موارد نیز مشابه با تفسیر نتایج ستون است.
نویسندگان:
هادی اسلام نیا
گلشید شید






2 پاسخ
سلام. آموزشتون تا حد زیادی به من کمک کرد. با این قیمتهای نجومی آموزشها، از اینکه آموزش رایگان قرار دادید سپاسگزارم.
سلام
ما هم خدمات رایگان و هم غیر رایگان داریم که هرکس بر اساس نیاز و شرایط خودش بتونه استفاده کنه. خوشحالیم که این آموزش ها برای شما مفید بوده